Differential graded category

In mathematics, especially homological algebra, a differential graded category or DG category for short, is a category whose morphism sets are endowed with the additional structure of a differential graded Z-module.

In detail, this means that 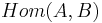$Hom(A,B)$ , the morphisms from any object A to another object B of the category is a direct sum 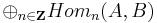$\oplus_{n \in \mathbf Z}Hom_n(A,B)$ and there is a differential d on this graded group, i.e. for all n a linear map 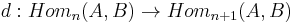$d: Hom_n(A,B) \rightarrow Hom_{n%2B1}(A,B)$ , which has to satisfy 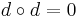$d \circ d = 0$ . This is equivalent to saying that 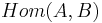$Hom(A,B)$ is a cochain complex. 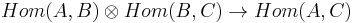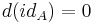Furthermore, the composition of morphisms $Hom(A,B) \otimes Hom(B,C) \rightarrow Hom(A,C)$ is required to be a map of complexes, and for all objects A of the category, one requires $d(id_A) = 0$ .

Examples

Any additive category may be considered to be a DG-category by imposing the trivial grading (i.e. all $\mathrm{Hom}_n(-,-)$ vanish for n ≠ 0) and trivial differential (d = 0).
A little bit more sophisticated is the category of complexes 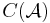$C(\mathcal A)$ over an additive category 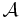$\mathcal A$ . By definition,

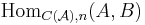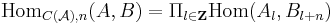$\mathrm{Hom}_{C(\mathcal A), n} (A, B)$ is the group of maps $A \rightarrow B[n]$ which do not need to respect the differentials of the complexes A and B, i.e. $\mathrm{Hom}_{C(\mathcal A), n} (A, B) = \Pi_{l \in \mathbf Z} \mathrm{Hom}(A_l, B_{l%2Bn})$ . The differential of such a morphism 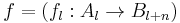$f = (f_l�: A_l \rightarrow B_{l%2Bn})$ of degree n is defined to be 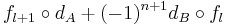$f_{l%2B1} \circ d_A %2B (-1)^{n%2B1} d_B \circ f_l$ , where 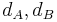$d_A, d_B$ are the differentials of A and B, respectively. This applies to the category of complexes of quasi-coherent sheaves on a scheme over a ring.

A DG-category with one object is the same as a DG-ring.

Further properties

The category of small dg-categories can be endowed with a model category structure such that weak equivalences are those functors that induce an equivalence of derived categories.^[1]

Given a dg-category C over some ring R, there is a notion of smoothness and properness of C that reduces to the usual notions of smooth and proper morphisms in case C is the category of quasi-coherent sheaves on some scheme X over R.

References

^ Tabuada, Gonçalo (2005), "Invariants additifs de DG-catégories", International Mathematics Research Notices (53): 3309–3339, doi:10.1155/IMRN.2005.3309, ISSN 1073-7928, http://dx.doi.org/10.1155/IMRN.2005.3309

Keller, Bernhard (1994), "Deriving DG categories", Annales Scientifiques de l'École Normale Supérieure. Quatrième Série 27 (1): 63–102, ISSN 0012-9593, MR 1258406, http://www.numdam.org/numdam-bin/fitem?id=ASENS_1994_4_27_1_63_0